Thanks for Reading 😊 This project is using a .NET Core WPF App on the .NET 6.0 framework with C# and HTML
LOGIC public class GameGrid The constructor will use the number of rows and columns as parameters
IsInside checks if row or column is inside the GameGrid r must be >=0 and < the number of Rows c must be >=0 and < the number of Columns
IsEmpty checks if a cell IsInside and the value of the array == 0
IsRowFull If any tile on the row is 0 then return false If no tile is 0 then return true and the MoveRowDown method is used
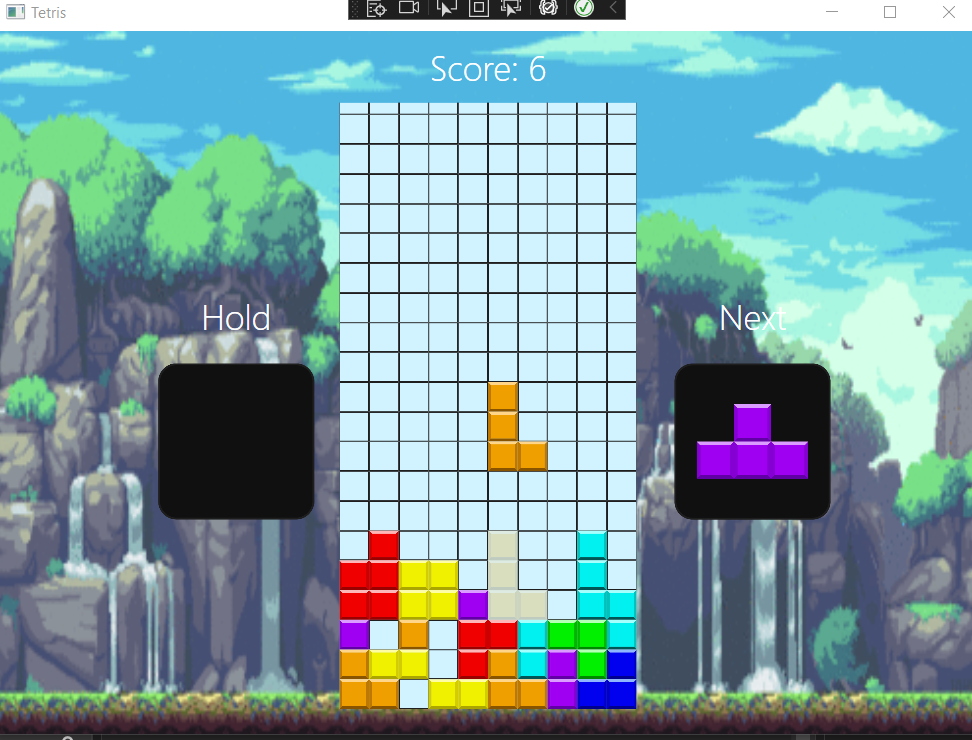
ClearFullRows Checks 0 row and loops through each row until no rows are full then value of Cleared is stored and all rows move down that value This clearing method is how the score is kept !
public class Position The Block offset is relative to the block matrix size Each unique block matrix must have its own offset parameters The origin is in the top left corner of the 22 by 10 Main matrix
public abstract class Block This Includes subclasses of each specific block Each block is represented in their respective matrix size with a 2d array
IEnumerable This method loops over the tile positions in the current rotaionState then adds the row offset and column offset
RotateCW - 90 degrees clock-wise RotateCCW - 90 degrees counter clock-wise
| 22 by 10 GameGrid Space |
|---|
| I -Block Matrix Size 4*4 |
|---|
| 4*4 |
| GameGrid Starting position : ( -1 , 3 )** |
| { new(1,0), new(1,1), new(1,2), new(1,3) }, |
| { new(0,2), new(1,2), new(2,2), new(3,2) }, |
| { new(2,0), new(2,1), new(2,2), new(2,3) }, |
| { new(0,1), new(1,1), new(2,1), new(3,1) } |
| O -Block Matrix Size 2*2 |
|---|
| 2*2 |
| GameGrid Starting position : ( 0 , 4 )*** |
| { new(0,0), new(0,1), new(1,0), new(1,1) } |
| J -Block Matrix Size 3*3 |
|---|
| 3*3 |
| GameGrid Starting position : ( 0 , 3 ) |
| {new(0, 0), new(1, 0), new(1, 1), new(1, 2)}, |
| {new(0, 1), new(0, 2), new(1, 1), new(2, 1)}, |
| {new(1, 0), new(1, 1), new(1, 2), new(2, 2)}, |
| {new(0, 1), new(1, 1), new(2, 1), new(2, 0)} |
| L -Block Matrix Size 3*3 |
|---|
| 3*3 |
| GameGrid Starting position : ( 0 , 3 ) |
| {new(0,2), new(1,0), new(1,1), new(1,2)}, |
| {new(0,1), new(1,1), new(2,1), new(2,2)}, |
| {new(1,0), new(1,1), new(1,2), new(2,0)}, |
| {new(0,0), new(0,1), new(1,1), new(2,1)} |
| s -Block Matrix Size 3*3 |
|---|
| 3*3 |
| GameGrid Starting position : ( 0 , 3 ) |
| { new(0,1), new(0,2), new(1,0), new(1,1) }, |
| { new(0,1), new(1,1), new(1,2), new(2,2) }, |
| { new(1,1), new(1,2), new(2,0), new(2,1) }, |
| { new(0,0), new(1,0), new(1,1), new(2,1) } |
| T -Block Matrix Size 3*3 |
|---|
| 3*3 |
| GameGrid Starting position : ( 0 , 3 ) |
| {new(0,1), new(1,0), new(1,1), new(1,2)}, |
| {new(0,1), new(1,1), new(1,2), new(2,1)}, |
| {new(1,0), new(1,1), new(1,2), new(2,1)}, |
| {new(0,1), new(1,0), new(1,1), new(2,1)} |
| Z -Block Matrix Size 3*3 |
|---|
| 3*3 |
| GameGrid Starting position : ( 0 , 3 ) |
| {new(0,0), new(0,1), new(1,1), new(1,2)}, |
| {new(0,2), new(1,1), new(1,2), new(2,1)}, |
| {new(1,0), new(1,1), new(2,1), new(2,2)}, |
| {new(0,1), new(1,0), new(1,1), new(2,0)} |
**negative positions are represented to spawn in blocks on the top portion of the grid that is not visible to the user *** The O Block is only a 2 by 2 matrix therefore it will spawn more ‘inward’ at ( 0, 4 ) on the GameGrid
| Id |
|---|
| 0 -blank |
| 1 -cyan |
| 2 -blue |
| 3 -orange |
| 4 -yellow |
| 5 -green |
| 6 -purple |
| 7 -red |