Convex hull of two zonotopes

[mforets]

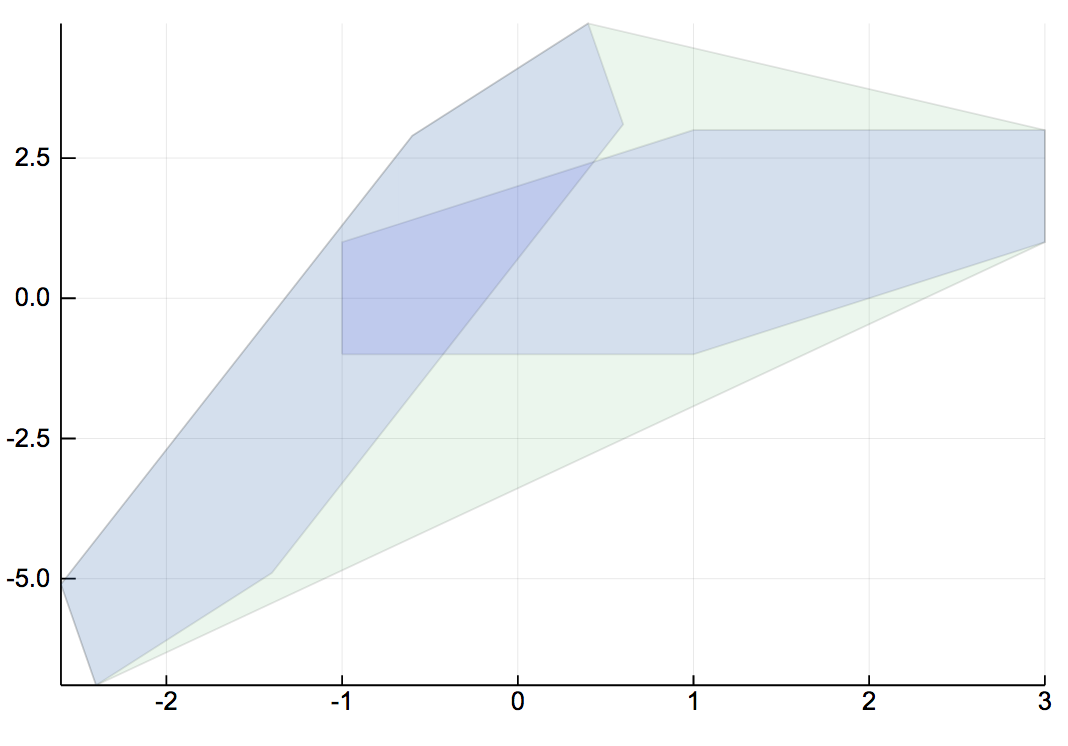
If Z1 and Z2 are zonotopes, their convex hull is a polytope but not a zonotope, in general. For instance, let:

using LazySets, Plots
Z1 = Zonotope(ones(2), [[1., 0.], [0., 1.], [1., 1.]])
Z2 = Zonotope(-ones(2), [[.5, 1.], [-.1, .9], [1., 4.]])
Y = ConvexHull(Z1, Z2)

plot([Z1, Z2], alpha=.1)
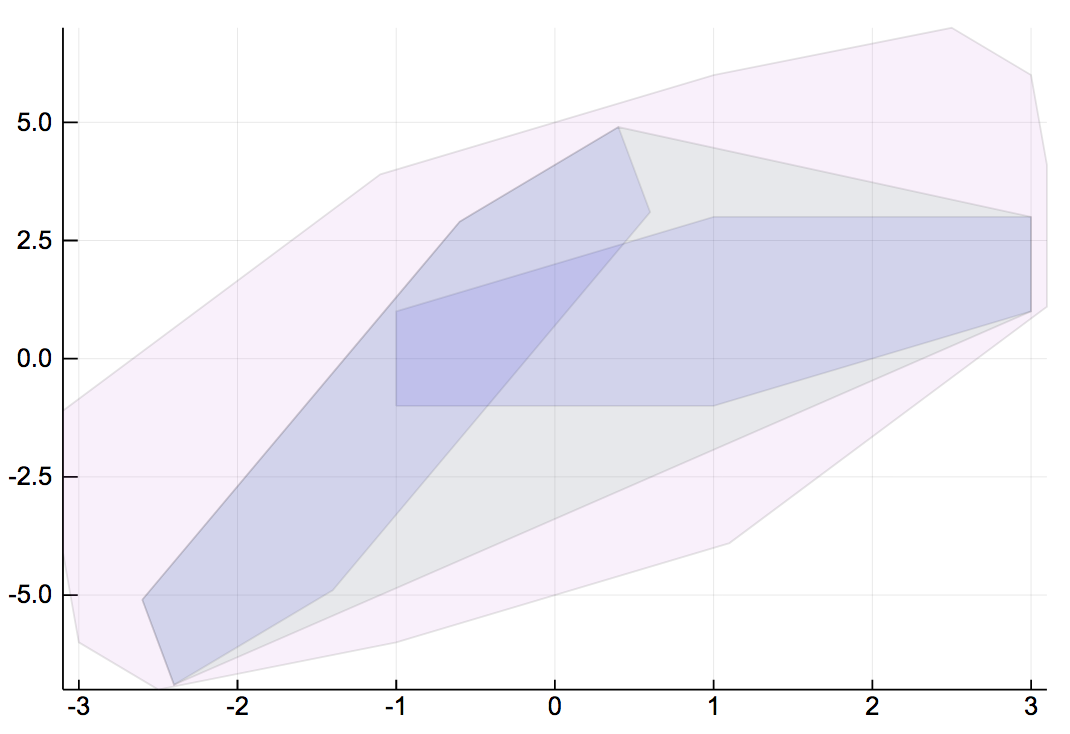
plot!(Y, 1e-2, alpha=.1)

The convex hull Y was computed above using a polygonal approximation. As discussed in [Reachability of Uncertain Linear Systems Using Zonotopes, A. Girard, HSCC 2005], the set Y can be overapproximated with a zonotope as follows:

center = (Z1.center+Z2.center)/2
generators = [(Z1.generators .+ Z2.generators) (Z1.center - Z2.center) (Z1.generators .- Z2.generators)]/2
Z3 = Zonotope(center, generators)
plot!(Z3, alpha=0.1)

It is also noted that Z3 is not necessarily the minimal enclosing zonotope, which is in general expensive in high dimensions and it is investigated in [Zonotopes as bounding volumes, L. J. Guibas et al, PRoc. of Symposium on Discrete Algorithms, pp 803-812].

---

We could define:

function overapproximate(S::ConvexHull{N, Zonotope{N}, Zonotope{N}}, ::Type{<:Zonotope})::Zonotope where {N<:Real}
    Z1, Z2 = S.X, S.Y
    center = (Z1.center+Z2.center)/2
    generators = [(Z1.generators .+ Z2.generators) (Z1.center - Z2.center) (Z1.generators .- Z2.generators)]/2
    return Zonotope(center, generators)
end

that implements this function. What do you think?

Another approach for the API is to introduce some sort of new name convex_hull_overapproximation.. but i think that it is better to exploit the existent ones (so long as we are coherent).

[schillic]

I wonder if the restriction to the ConvexHull type is good. What about ConvexHullArray? Does this method generalize to n-ary hulls?
A function convex_hull_overapproximation should take two Zonotopes and do both the hull and the overapproximation, right? In this sense it is more general.

But this is really a very special case, and since you already have the code, you can add it :)

[mforets]

the convex hull array of zonotopes could indeed be added as well (since it is parametric in both N and S, that's easy).

up to now we've been using overapproximate to work for 2D sets only. do you see some inconvenience of using it for high dimensions? (it is worth mentioning that extending the iterative refinement method to higher dims is not discarded.) i don't see problems ahead; and note that the name overapproximate is almost an alias of approximate, since:

function overapproximate(S::LazySet, ɛ::Real)::HPolygon
    @assert dim(S) == 2
    return tohrep(approximate(S, ɛ))
end

we would need at least to rename the file 2D_approximations.jl -> overapproximate.jl or overapproximations.jl

[schillic]

I do not see any obstacles for using it in higher dimensions. This is also eventually required for #136. It might be convenient to have a more general interface that automatically chooses HPolygon for 2D and HPolytope for higher dimensions.

[schillic]

Agreed with the renaming of 2D_approximations.jl. Both options are fine, though I prefer overapproximate.jl a bit if there are only overapproximate methods inside.

[mforets]

the zonotope arguments should have the same number of generators (and dimension). proposal: add an @assert order(..) on overapproximate(S::ConvexHull{N, Zonotope{N}, Zonotope{N}}, ::Type{<:Zonotope})::Zonotope where {N<:Real}